Cosine

Cosine similarity a measure of similarity between two non-zero vectors defined in an inner product space. Cosine similarity is the cosine of the angle between the vectors; that is, it is the dot product of the vectors divided by the product of their lengths.

The cosine of two non-zero vectors can be derived by using the Euclidean dot product formula:

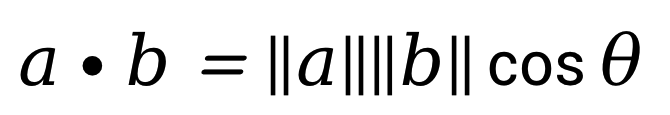
Given two n-dimensional vectors of attributes: A and B, the cosine similarity, cos(Θ), is represented using a dot product and magnitude as:

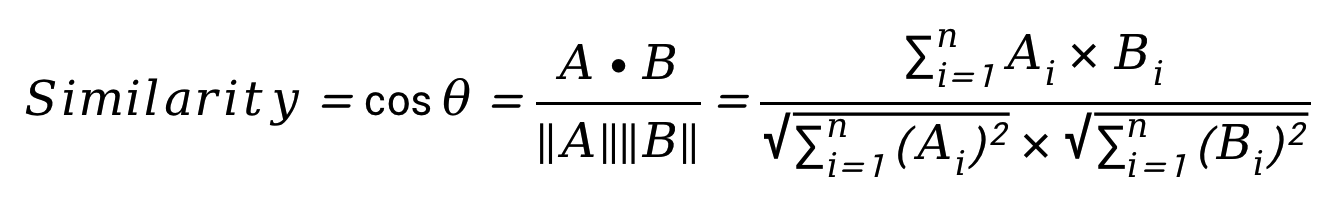
Ai and Bi shown above represents vector components of vector A and B. The resulting similarity ranges from -1 meaning exactly opposite, to 1 meaning exactly the same, with 0 indicating orthogonality or decorrelation, while in-between values indicate intermediate similarity or dissimilarity.

Normalization

Normalization is a data preparation technique that is frequently used in machine learning. The goal of normalization is to transform features to be on a similar scale. This improves the performance and training stability of the model. Normalization in machine learning is the process of translating data into the range [0, 1] (or any other range) or simply transforming data onto the unit sphere. L2 normalization is a technique that modifies the dataset values in a way that in each row the sum of the squares will always be up to 1. It is also called least squares.

L2 Normalization is performed against every dimensional data, X1, X2,...,Xn, of vector X, each will be divided by ||X||2 to get a new vector

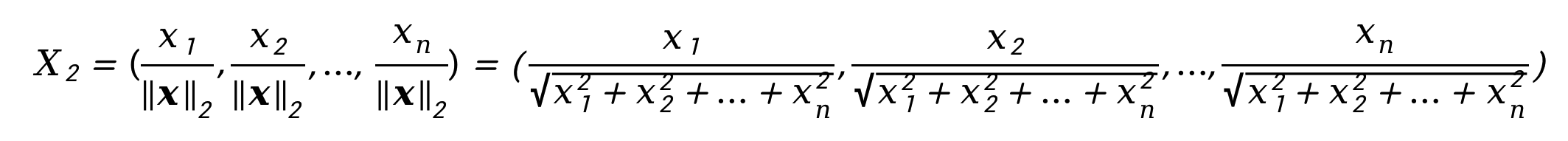
If vector A=(2,3,6), we can get that:

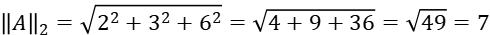
Thus a new vector after L2 Normalization will be:

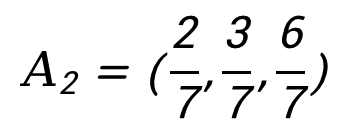
Obviously, the inner product of normalization is closely related to cosine distance.